The 1997 Academy award winning movie Good Will Hunting is about a troubled genius named Will Hunting, played by Matt Damon. During initial run of the movie, we came across two mathematical problems stated by MIT professor, and are solved by Will. Out of the two problems, we will be looking at the second problem when we see Will get caught solving it.
The math problem is stated as below :
a) How many trees are there with n labeled vertices ?
b) Draw all homomorphically irreducible trees with n = 10.Solutions:
a) In order to get answer for number of trees with n labeled vertices, we need to know Cayley's formula. It is an important result in Graph theory.
It states that for every positive integer n, the number of trees on n labeled vertices is n^(n-2)
Source : Wikipedia
b) Let us understand question before we dive into solution of it. We will understand first the terms used in the problem. Let us think it as a puzzle with following nomenclature used to describe it and conditions to follow.
What are trees ?
Simply, trees can be called as networks of dots and lines.
But, we have to find trees with an additional conditions as follows:
1. Homomorphism is to be followed.What is to be done exactly when it is said to follow homomorphism?
The above two trees each with size 6 are homomorphically same. Just what is done is little bit of twisting. So, you can’t count these as separate. In the same context, the mirror images are also treated as homeomorphically same, as below. So, you need to count it as one.
2. Cyclic structure is not allowed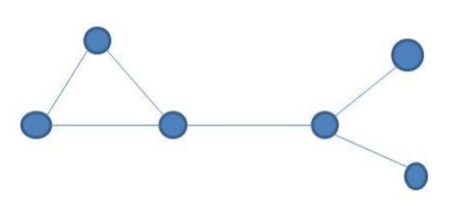
The above tree contains cyclic structure i.e. triangular one. It is not allowed.
3. It should be irreducible.
Clearly, you can understand that the middle red dot can be reduced just by eliminating it and joining the adjacent two blue dots by a line. It is reducible. No such trees are allowed.
Thus, the following are all homomorphically irreducible trees with n = 10 , taking into consideration above conditions.
Thus, there are 10 homomorphically irreducible trees with n = 10.
Comments