The quadratic equations are introduced to us in the early days of elementary school. It's one of the fundamental forms of equation in algebra. It is represented as follows.
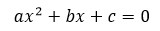
x is referred as unknown in the equation, where as a, b, c are known as quadratic, linear and constant term of the given quadratic equation respectively.
If the roots of the quadratic equation are r and s, we get,
ax^2 + bx + c = (x - r)(x - s) Traditionally, we have been solving the above quadratic equation as
We first make leading coefficient i.e. a to 1 by dividing the whole equation by a.
1. Trial and error factorization method
Where in we try to find the values of r and s in such a way that the sum of the roots is (-b) and the product of the roots is c.
2. Quadratic formula
The quadratic formula is widely used and directly provides real and imaginary roots of the quadratic equation with the help of following formula:
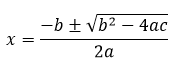
Recently, Po-Shen Loh, a professor at Carnegie Mellon university, pioneered a new algorithmic technique to solve the quadratic equations. This newly found method was used by ancient Babylonians around 4000 years ago.
The new Loh's method to solve the quadratic equations is as follows:
For given quadratic equation of the form Ax^2 + Bx + C = 0;
(Make the leading coefficient one (A = 1) if A != 1 by dividing the whole equation by A.)
1. Let r and s be the roots of the quadratic equation x^2 + bx + c = 0.
2. The roots r and s are given as
r = (-b/2) + u
s = (-b/2) - u
3. The product of the roots is c.
r * s = c
4. So, solving for variable u,
(-0.5b + u)(-0.5b - u) = c
5. Substitute the value of u in the equations of r and s to find the roots of the quadratic equation.
The method is fundamentally same as the quadratic formula but provides an alternative to find the roots by following few steps instead of the formula which one may find cumbersome to remember.
Comments