Fermat's Last Theorem and Andrew Wiles
- Aniruddha Anant

- Jul 23, 2021
- 6 min read
Updated: Aug 5, 2021
Fermat's last theorem is one of the most difficult and widely discussed problems in the history of mathematics. It has got the largest number of unsuccessful proofs and thus is mentioned in the Guinness Book of World records as the 'most difficult mathematical problem'. The beauty of this problem is that it is simple enough to be understood by a kid doing elementary mathematics and yet difficult to prove for even a well-established mathematician. So, before delving right into the statement of Fermat's Last theorem, we will approach it step-by-step with the understanding of some fundamental terminologies.
Let us start by looking at the following diagram.
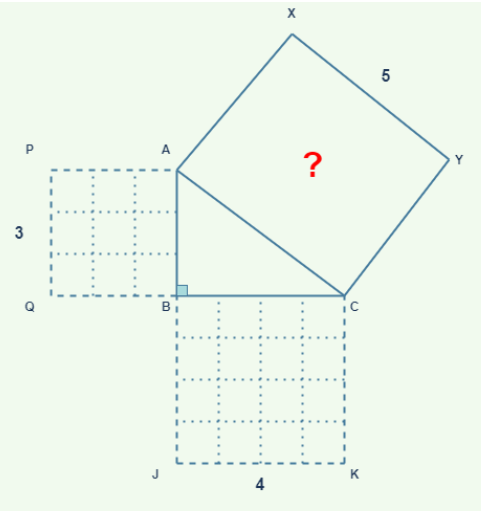
For a given right-angled triangle ABC, we perform a few constructions. We draw squares on each side of the triangle, namely squares APQB, BJKC, and CYXA and then we further partition the squares into unit squares. Thus if in the diagram the squares APQB and BJKC are partitioned into 9 and 16, then how many unit squares would square CYXA contain?
The number of unit squares in CYXA = Number of unit squares in APQB + Number of unit squares in BJKC.The answer is 25. Many of us might have been introduced with the above diagram earlier as a geometrical representation of the famous Pythagoras theorem.
For Triangle ABC, where angle B = 90 degrees, the following equation holds true,
AB * AB + BC * BC = CA * CA Have you ever wondered what if we extend this idea of constructing squares in a higher dimension, say, 3-dimension? What if we construct cubes on each surface of the triangle?
Will the sum of the volume of the cubes constructed on the side surfaces of a triangle be equal to the volume of the cube constructed on the hypotenuse surface of the triangle?

For given 3 dimensional figure, will the following equation hold true?
AB * AB * AB + BC * BC * BC = CA * CA * CA Well, the answer is No. Why? Let's see if we can find why.
Now moving further ahead, what if we try to generalize the above equation for variable n as follows,
For any integer value of n, will the equation a^n + b^n = c^n hold true when a, b and c are three positive integers? And, that's what Fermat's last theorem is about. It is stated as follows:
No three positive integers a, b, and c satisfy the equation a^n + b^n = c^n for any integer value of n greater than 2. This is also referred to as Fermat's conjecture in older books because it was first stated by, a French mathematician, Pierre de Fermat in 1637 and was not proved until a long time.

Interestingly enough, Fermat has stated this theorem in a margin of his copy of the book Arithmetica with a note as "Hanc marginis exiguitas non caperet, Demonstrationem mirabilem" which translates as "I have a truly marvelous demonstration of this which this margin is too narrow to contain." And, right after that, one of the intriguing and wonderful journeys began in the mathematical world.
Nowadays, one can easily say that we can prove this with what we have as supercomputers by checking various values of n up to billions. This technique of brute force is not useful when it comes to mathematical rigorous proof. Just to get the sense of rigorosity, let us go through the following well-known joke of sheep in Scotland.
A mathematician, a physicist, and an engineer are riding a train through Scotland.
The engineer looks out the window, sees a black sheep, and exclaims, "Hey! They've got black sheep in Scotland!"
The physicist looks out the window and corrects the engineer, "Strictly speaking, all we know is that there's at least one black sheep in Scotland."
The mathematician looks out the window and corrects the physicist, " Strictly speaking, all we know is that at least one side of one sheep is black in Scotland."So, in our case, if we consider n = 2 in FLT, we know, there exist values of a, b, and c which is called Pythagorean triples. Now, consider the following right-angled triangle ABC.
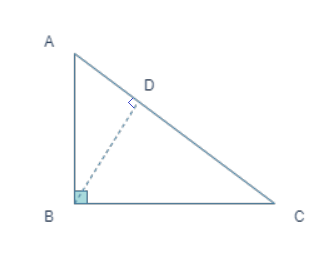
Construction: Draw a perpendicular line BD from the vertex B of the right angle onto hypotenuse AC.
In triangle ADB and triangle ABC,
Angle A is common.
Angle ADB = Angle ABC = 90 degrees
Hence, by AA test of similarity test of triangle, we get,
triangle ABC ~ triangle ADB
AC/AB = AB/AD
AB * AB = AD * AC ------------------------------(1)
In triangle BDC and triangle ABC,
Angle C is common.
Angle BDC = Angle ABC = 90 degrees
Hence, by AA test of similarity test of triangle, we get,
triangle ABC ~ triangle BDC
BC/DC = AC/BC
BC * BC = DC * AC ------------------------------(2)
Using the results (1) and (2), we get,
AB^2 + BC^2 = (AD + DC) * AC
AB^2 + BC^2 = AC^2 , thus proving Pythagoras theorem.
AB, BC and AC as (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37) are few Pythagorean triplets. And, we can always find the next triplet by brute force. Hence, instead of brute force, what we need is rigorous proof of the Pythagoras theorem as stated above.
Similarly, mathematicians were trying to find the rigorous proof of Fermat's last theorem. In fact, the reason it is called as Fermat's Last Theorem is because it was the last remaining problem among problems stated by Pierre Fermat that anyone can construct the proof for.
Meanwhile many were attempting to solve the problem, there happened the start of an important journey when a 10-year-old kid named Andrew, now Sir Andrew Wiles, came across a book "The Last Problem" by E. T. Bell. He understood the problem and got interested by the fascinating history of Fermat's last theorem. On searching the proof, he could only find that it is unproven for more than three centuries despite many attempts by a lot of great mathematicians. Later, when he had his formal education in the field of Number theory, he decided and accepted the challenge to prove Fermat's last theorem. He worked on the problem for six years in complete secrecy. There were some years when he knew he was on the right track, but it could be that the tools needed to solve were beyond present-day mathematics then. Quoting Andrew Wiles, "..So even if I was on right track, I could be living in the wrong century." Despite a lot of hurdles, he kept on trying and achieving small breakthroughs, thus, constructing the proof day by day. Finally, when he had completed the proof in the year 1992-93, he arranged a general lecture series of three days at the Cambridge conference and presented his proof stating in the conclusion that Fermat's last theorem is true! And, the world was shocked. None was anticipating that the general talk by Andrew is going to have such an important and beautiful conclusion for which the world was waiting for centuries!
Instead what was required was a logical step-by-step argument which would effectively give a reason and explain why every elliptic equation had to be modular….. “I carried this thought around in my head basically the whole time. I would wake up with it first thing in the morning, I would be thinking about it all day and I would be thinking about it when I went to sleep. Without distraction I would have the same thing going round and round in my mind.” – Andrew Wiles on his quest to find the proof of Fermat's Last Theorem (A book : Fermat’s last theorem, by Simon Singh).
Though the proof was complete, it was being verified and checked. And, it was discovered that there is one slight problem with the proof. Andrew decided to give it a try but couldn't fix the problem. Luckily, when he was about to give up, after a year, in 1994, he could crack the problem and published the complete proof along with his student Richard Taylor.
“I was casually looking at a paper of Barry Mazur’s and there was one sentence there that just caught my attention. It mentioned a nineteenth-century construction, and I suddenly realized that I should be able to use that to make the Kolyvagin–Flach method work on the final family of elliptic equations.” - Andrew Wiles on fixing the slight mistake in the proof.
At last, Fermat's Last Theorem was proved and it took 358 years to achieve the first successful proof having 200 pages of advanced number theory which was released by Sir Andrew Wiles.
“This was my childhood passion, dream. …Having solved this problem there’s certainly a sense of loss, but at the same time there is this tremendous sense of freedom. I was so obsessed by this problem that for eight years I was thinking about it all the time – when I woke up in the morning to when I went to sleep at night. That’s a long time to think about one thing. That particular odyssey is now over. My mind is at rest.” - Andrew Wiles
Andrew Wiles collected the Wolfskehl prize for his work on Fermat's last theorem in 1997. He has also been awarded Abel Prize in 2016 for proving Fermat's last theorem.
The proof presented by Sir Andrew Wiles contains techniques beyond 17th-century mathematics. So, the mystery remains whether Fermat had the marvelous proof of his theorem for which the margin was too narrow to contain!




Comments